In this article, we outline and explain the principles behind tokenization and how this is used by financial institutions in transaction processing all over the world. Billions of personal records, including credit card data and personally identifiable information (PII) needs to be secure from cybersecurity disasters and exposure to data breach risk. One method is by using tokenization.
What exactly is tokenization: General principle
Tokenization is the process of replacing sensitive data with symbols that retain all of the vital information about the data without compromising its security.
Tokenization is quite ancient and present in everyday life. Here are valid examples of tokenization:
- a social security number represents a citizen,
- a number represents a Swiss “numbered” bank account,
- a labelled plastic token represents real money deposited at the casino’s bank,
- a nickname (pseudonyme, nom de plume, nom de guerre) and so on...
Tokenization is the generalisation of a cryptographic hash. It means representing something by something else, a symbol (‘token’), which will be substituted to the original entity.
In the more precise context of cryptography, a token is a symbol (or a group of symbols) which represents sensitive information in such a way that no useful information can be retrieved from the value of that symbol. It’s not exactly the same concept as encryption because actually the symbol which is substituted can mean something. The idea is more confusion (in the sense of luring attackers) and indeed substitution.
A cryptographic token is then a sort of proxy symbol that acts on behalf of some sensitive information without allowing directly the exposure of that confidential information.
A very commonly used tokenization in computers is the hashing of the passwords. Indeed computers since the old ages store the passwords of users as hashes.
Often, tokenization will be using the one-way cryptographic hashes, but it’s not a general rule and substitutions tables are also a valid way of performing tokenization.
A token can also be a graphical representation, an image. A substitution table provides a simple way of performing tokenization. This is often the principle of monoalphabetic substitution ciphers (Caesar’s cipher etc …)
For example we can represent each letter of the english alphabet (+ the space character) by a colour code (some colours may look the same but actually these are all different colours).
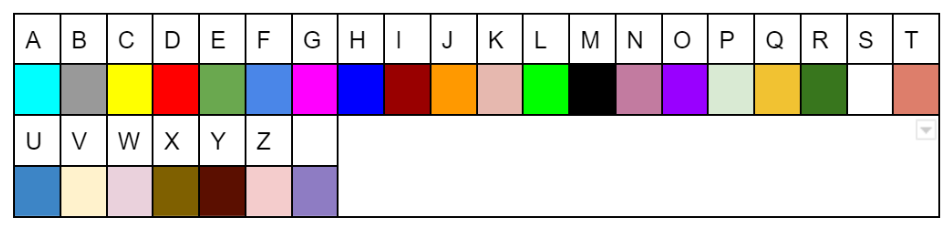
Instead of writing the confidential information “MR JOHNSON” which could be the name of a important person for instance, we will represent it by the following token:

Not knowing the substitution table, that colour code is completely unintelligible. There is no way to use it.
We could also use symbols such as smileys for instance.
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T |
| 😛 | 🤭 | 😍 | 😃 | 🤗 | 😆 | 🤑 | 🙃 | 🤣 | 😄 | 😚 | 😗 | 😊 | 😁 | 🤩 | 🥰 | 😆 | 😋 | 😂 | 🤪 |
| U | V | W | X | Y | Z | ||||||||||||||
| 😝 | 😀 | 😇 | 😜 | 🙃 | 🙂 | 😘 |
And the same sentence as in the previous example would be replaced by the following token:
| 😊 | 😋 | 😘 | 😄 | 🤩 | 🙃 | 😁 | 😂 | 🤩 | 😁 |
All these examples show that token aims at confusing and eventually at luring an eventual attacker.
Tokenization vs Encryption: why it's not the same
Tokenization is different from encryption and in fact they are complementary concepts.
Tokenization can be viewed as an encryption requiring the usage of a big dictionary linking entries and tokens. Without that big dictionary, reversing tokens to their original entries is usually hardly possible or even totally impossible.
But “standard” cryptographic functions like AES or RSA can also be effectively used in order to generate tokens. There will be no need for any dictionary and the knowledge of the key(s) will be enough to map an entry with its token.
Finally and less obvious, “pure'' random functions can be used to generate tokens, in combination with a dictionary mapping a value to its token generated by a random function. This is probably the best and ideal way to create tokens.
The main algorithms behind tokenization
As mentioned earlier, there are several ways of generating tokens:
- Hash functions
- Encryption
- Random functions
- Custom substitution tables
To have the ability to map a token to its real value, one must maintain a dictionary, except for algorithms using encryption or any reversible algorithm. Of course in such a case, the algorithms must provide a bijection, e.g a one-to-one correspondence. The place where the tokens are generated and eventually reversed is called the token vault.
In turn, token providers will use specific algorithms and especially format-preserving mechanisms, so that a token has the same format as the value that it represents. For example, a 16 digits bank account number should be represented by a 16 digit token. This is usually required so as not to break existing systems and to migrate them seamlessly to tokenization.
Here are what token providers generally use:
- Random number generator with “good” randomness. This means for instance passing successfully the die hard/ or die harder randomness tests;
- Random permutations from the space of the original values to the space of the tokens which follow the FIPS 140-2 Level 3 Random Number Generators standards;
- Random permutations that follow the NIST SP 800-90A Rev. 1 standard;
- Format preserving encryption (FPE) following the NIST 800-38G Rev. 1 standard (algorithm FF1);
- Cryptographic hashes using a cryptographic salt respecting the standards NIST 800-131a Rev. 2
Why Tokenization is not so easy
It could seem that tokenization is not so hard… after all, the concept is fairly simple, and any standard programmer can code a hash function which transforms any sort of information into tokens. This is a mistake! Here are some of the design issues which challenge a good token generation service:
- The token vault. The vault is where the dictionary information versus token is maintained and therefore must be ultra-secure. The dictionary must be safeguarded and possibly encrypted.
- Collision-free. The tokens should be collision-free otherwise there will be a risk that the wrong account may be charged in lieu of the right one!
- Speed. The token generation and comparaison in the vault must be fast.This is not so easy when working with millions of entries.
- No “Rainbow Tables”. The dictionary information/token should not be possibly re-created.
The benefits of Tokenization for payments
In the banking industry, the PCI-DSS requirements usually command or recommend in a greatest number of cases that credit card information, sensitive by nature, is tokenized and stored on databases. The EMV consortium has issued specifications regarding tokenization in EMV transactions. Visa and other card schemes also have their own requirements regarding tokenization.
Most of the case, that tokenization targets the Primary Account Number (PAN):
A 16-digit PAN is replaced by a 16-digit token that is usually randomly generated.
For example instead of using the PAN:
4085-8800-8378-3527
the payment system will use the token:
1454-0989-2121-8954
The token is completely useless unless it can be de-tokenized to the original PAN.
Even if the data is leaked, this token can be easily changed without the hassle of blocking the impacted payment card and producing a new one. Another benefit of tokenization is the reduction of false decline because anti-fraud controls are less severe when tokenization is in place since the risks are lesser than with a “real” payment card number.
Because of the history of massive credit card leaks, tokenization of card data has been actively pushed by the actors of the retail banking industry and especially in the context of mobile payments.
In fact, currently, most, if not all, mobile payments are using some form of tokenization.
In the second part we will see some actual examples of tokenization systems in the context of the payment industry.
Related Solutions
The Utimaco KeyBRIDGE TokenBRIDGE offers a complete tokenization solution to prevent organisations from data loss and guarantees unique tokenization of assets without complicating security management.
TokenBRIDGE implements a secure, easy-to-manage Token Vault - the core of any tokenization solution.
About the author
Martin Rupp es criptógrafo, matemático y cibercientífico. Lleva 20 años desarrollando e implementando soluciones de ciberseguridad para bancos y organizaciones relevantes para la seguridad. Martin investiga actualmente la aplicación del aprendizaje automático y Blockchain en la ciberseguridad.




