All eyes are on NIST: Organizations worldwide are waiting in the wings for the final PQC standards to be published this summer.
Why the buzz? Well, quantum computers might be powerful enough to perform certain cryptanalysis algorithms that can break or significantly weaken cryptography currently in use. Specifically, a future real quantum computer might be able to execute Shor’s and Grover’s algorithm, resulting in breaking common public key cryptography we know today and weakening symmetric encryption.
In this blog post, we’ll look at the type of cryptography based on certain “hard mathematical problems” that are considered secure against quantum computers and can be used for public key cryptography use cases.
Learn More About Proven Defense Mechanisms Against Quantum Threats - Watch our Webinar

Breaking Public Key Cryptography – Why Quantum Computers could break RSA
Let's look at a simplified example of the mathematical problems on which today's most popular schemes are based:
The security of the currently used asymmetric cryptographic mechanisms is based on so called hard problems (a term from computer science). A hard problem is one that is assumed to be hard to solve efficiently by a classical computer. The most common ones are known as the RSA problem (prime factorization) and the discrete logarithm problem.
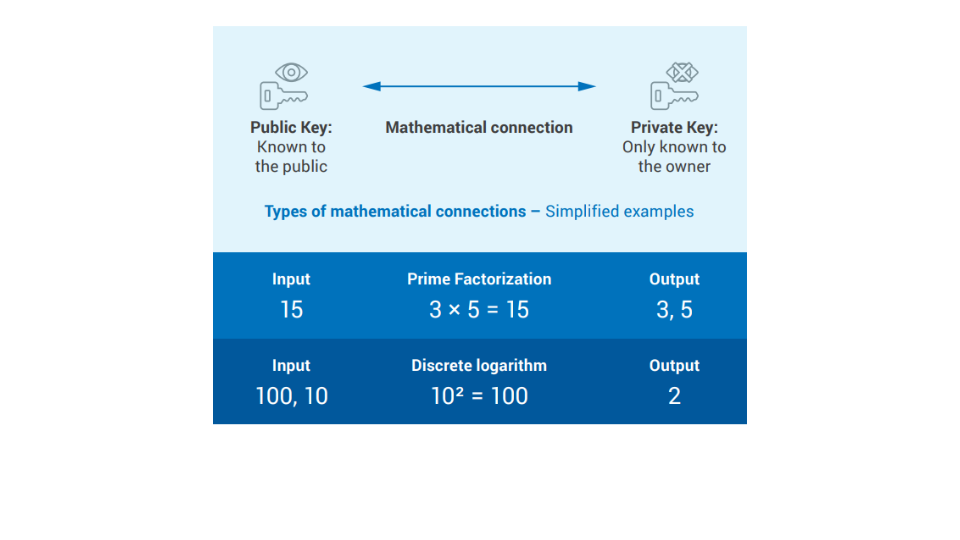
Shor’s algorithm presents a way to solve these difficult problems such as finding the prime factors of an integer in a more efficient way or calculating the discrete logarithm.
With this knowledge, an attacker could calculate the private key of most asymmetric cryptographic algorithms from the public key. This also affects RSA – one of the most used asymmetric methods. A quantum computer with a sufficient number of qubits (and other quantum computation properties) could operate Shor’s algorithm, allowing it to be used to break public key cryptographic schemes such as:
- RSA
- Elliptic-curve cryptography (ECC)
- Digital Signature Standard (DSS)
- Diffie–Hellman (DH) key exchange
This is why NIST started its post-quantum cryptography standardization project back in 2016.
Types of Quantum-Secure Cryptography Schemes
1. Hash-Based Cryptography
Use Case: Digital Signatures
Algorithms (popular examples):
- XMSS and the multi-tree variant XMSS-MT
- LMS and the multi-tree variant HSS
- SPHINCS+
Hash-based signature schemes are cryptographic primitives based on the security of hash functions which itself does not rely on the assumption of a computational hard problem. Furthermore, because they are based on an array of hash strings which are one-time signatures (OTS), they can only sign a predefined number of messages securely.
Learn more about stateful hash-based signature schemes.
2. Lattice-Based Cryptography
Use Case: Digital Signatures and Encryption / Key Encapsulation
Algorithms (popular examples):
- CRYSTALS-Kyber (ML-KEM)
- CRYTSALS-Dilithium (ML-DSA)
- FALCON
- Frodo-KEM
Lattices are mathematical structures consisting of a grid of regular points in a multi-dimensional space. The security relies on the hard problem of finding a vector in the lattice that is short. (Shortest Vector Problem and Closest Vector Problem)
Read more about Lattice-based cryptography.
3. Code-Based Cryptography
Use Case: Digital Signatures and Encryption / Key Encapsulation
Algorithms (popular examples):
- Classic McEliece
- BIKE
- HQC
Code-based cryptography is based on the hardness of problems from coding theory. In detail, the security relies on the hardness of decoding error-correcting codes.
Read more about code-based cryptography.
4. Multivariate-Based Cryptography
Use Case: Digital Signatures and Encryption / Key Encapsulation
Algorithms (popular examples):
- Rainbow (considered insecure as of now)
- GeMSS
- HFE
Multivariate cryptography schemes are based on the difficulty of solving systems of multivariate polynomials over a finite field.
Read more about Multivariate-based cryptography.
5. Isogeny-Based Cryptography
Use Case: Digital Signatures
Algorithms (examples):
- SIKE (considered insecure as of 2022)
- CSI-FiSh
- SIDH (considered insecure as of 2022)
- SQISign
Isogeny-based cryptography belongs to elliptic-curve cryptography, but the security relies on the problem of finding an explicit isogeny (rational map between elliptic curves) over a finite field.
Read more about Isogeny-based cryptography.
Look to the future – What to Expect from the NIST PQC Standardization Process
In April 2024, NIST held the 5th NIST PQC Standardization. During this conference, the submissions teams for BIKE, Classic McEliece, Falcon, and HQC gave an update on their algorithms. Several experts attended and discussed the algorithms and NIST received feedback which will be considered in the further standardization process. We expect an update on the round 4 algorithms from NIST in the summer of 2024.
Additionally, there is another, separate round for standardizing digital signature schemes.
There are currently 40 submissions accepted in the first round of evaluation. The entire evaluation and analysis process is expected to take several years.
Learn More About Proven Defense Mechanisms Against Quantum Threats - Watch our Webinar

About the Author
Lena Backes is an IT Marketing expert with more than 10 years of experience working in the B2B sector. In her professional career, she has gained extensive knowledge in various areas, including cybersecurity, network management, enterprise streaming, and software asset management. In her current role she is responsible for product positioning of Utimaco’s cybersecurity products and solutions, with a particular focus on data protection, blockchain technology, and post quantum cryptography.






