What is Hash-based Cryptography?

Definition: Hash-based cryptography was first developed by Leslie Lamport and Ralph Merkle in the late 1970s. Hash-based cryptography creates digital signature algorithms whose security is mathematically based on the security of a selected cryptographic hash function.

Hash-based Cryptography explained

A hash function is a unique identifier for any given piece of content. It’s also a process that takes plaintext data of any size and converts it into a unique ciphertext of a specific length. Hash functions take an input string (typically or an arbitrary length) and return a fixed-size “digest” as output. Common cryptographic hash functions like SHA2, SHA3 or Blake2 produce digests ranging from 256 bits to 512 bits.

A hash-based signature scheme starts from a one-time signature scheme (OTS) - a signature scheme where a key pair must only be used to sign one message. If an OTS key pair is used to sign two different messages, an attacker can easily forge signatures.

However, what Merkle proposed was a way to retain the ability to sign N different messages which works as follows:

1. First, create N separate Lamport keypairs. An example could be (PK_1, SK_1), \dots, (PK_N, SK_N)

2. Next, assign each public key to one leaf of a Merkle hash tree (see below) and compute the tree's root. This root will serve as the new Merkle signature scheme's "master" public key.

3. The signer retains all of the Lamport public and secret keys for use in signing.

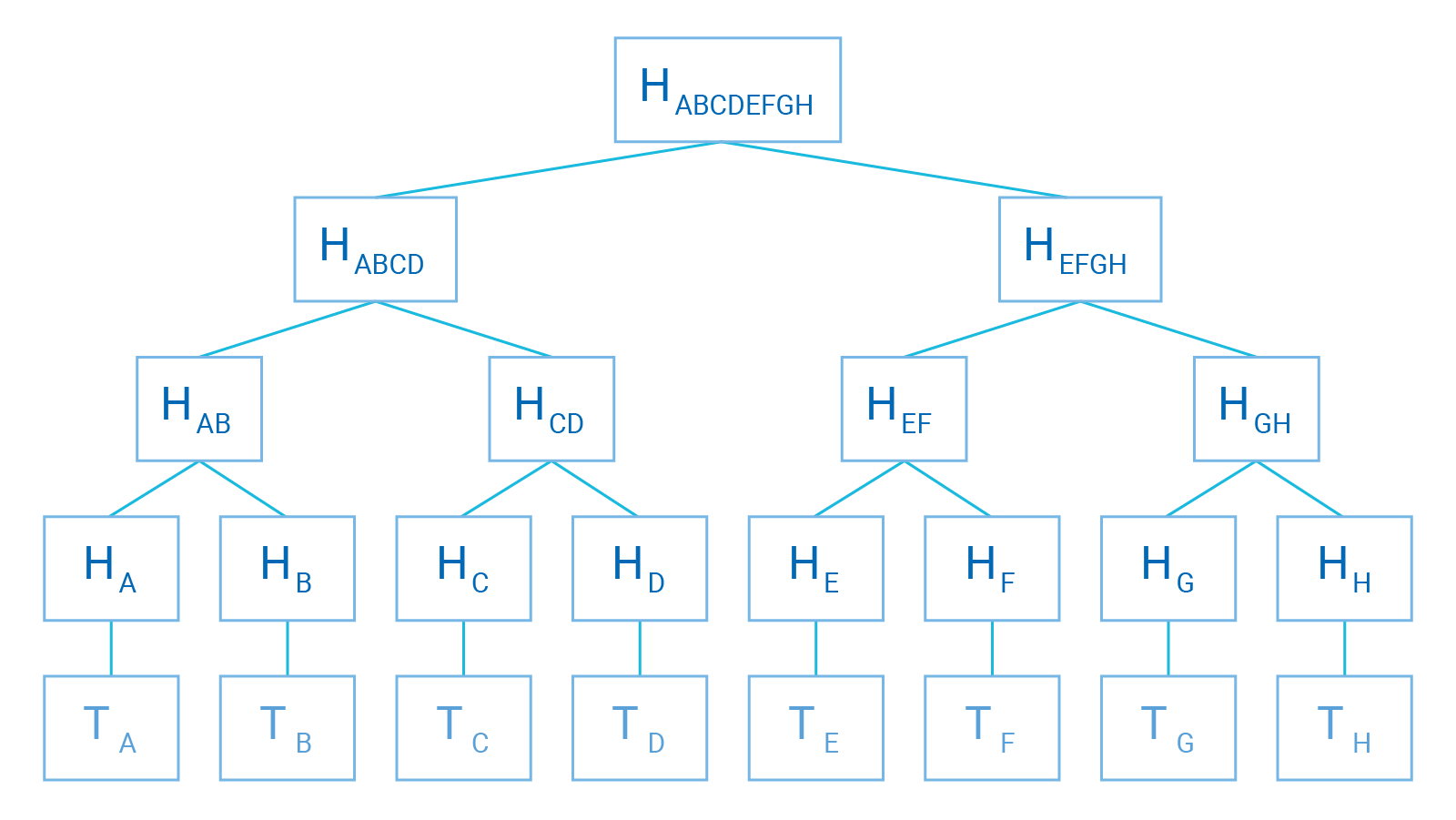
A Merkle tree (or hash tree) is a data structure that is represented as a tree in which each leaf node is labeled with the cryptographic hash value of a data block and each non-leaf node is labeled with the cryptographic hash of the labels of its child nodes. Hash trees enable efficient and secure verification of large data structures' contents.

Each block-level in the Merkle Tree above reflects a higher order of hashing stemming from a transaction (T0-T7). The succeeding hash value (H) is passed through a hash function for each block-level above the initial transaction until it reaches the highest block-level represented as the sum of all the preceding hashes (H01234567).

The lowest-level hash values are referred to as leaves, and they contain the hashed value of the transaction (T) that is associated with the leaf. Levels 3 and 4 are the results of the hashing of leaves and their subsequent hashes (or nodes). Lastly, the Merkle Root, the highest block-level, contains the summary of all transaction data as a single value.

Numerous hash-based signature schemes with improved performance have been invented since Merkle's initial approach. The XMSS, Leighton-Micali (LMS), SPHINCS, and BPQS schemes are recent examples. Unlike typical digital signature techniques, most hash-based signature schemes are stateful, which means that signing necessitates the update of the secret key.

Signing with stateful hash-based signature techniques necessitates keeping track of the utilized one-time keys and ensuring that they are never repeated. The schemes XMSS, LMS, and BPQS are stateful, but the SPHINCS scheme is stateless. Signatures in SPHINCS are larger than those in XMSS and LMS. BPQS was created with blockchain systems in mind. In addition to the WOTS+ one-time signature technique, SPHINCS employs the HORST few-time (hash-based) signature mechanism. HORST is an enhancement to an older few-time signature technique (Hash to Obtain Random Subset).

The three digital signature algorithms*, to be standardized by NIST (based on structured lattices) for quantum-safe digital signatures are: